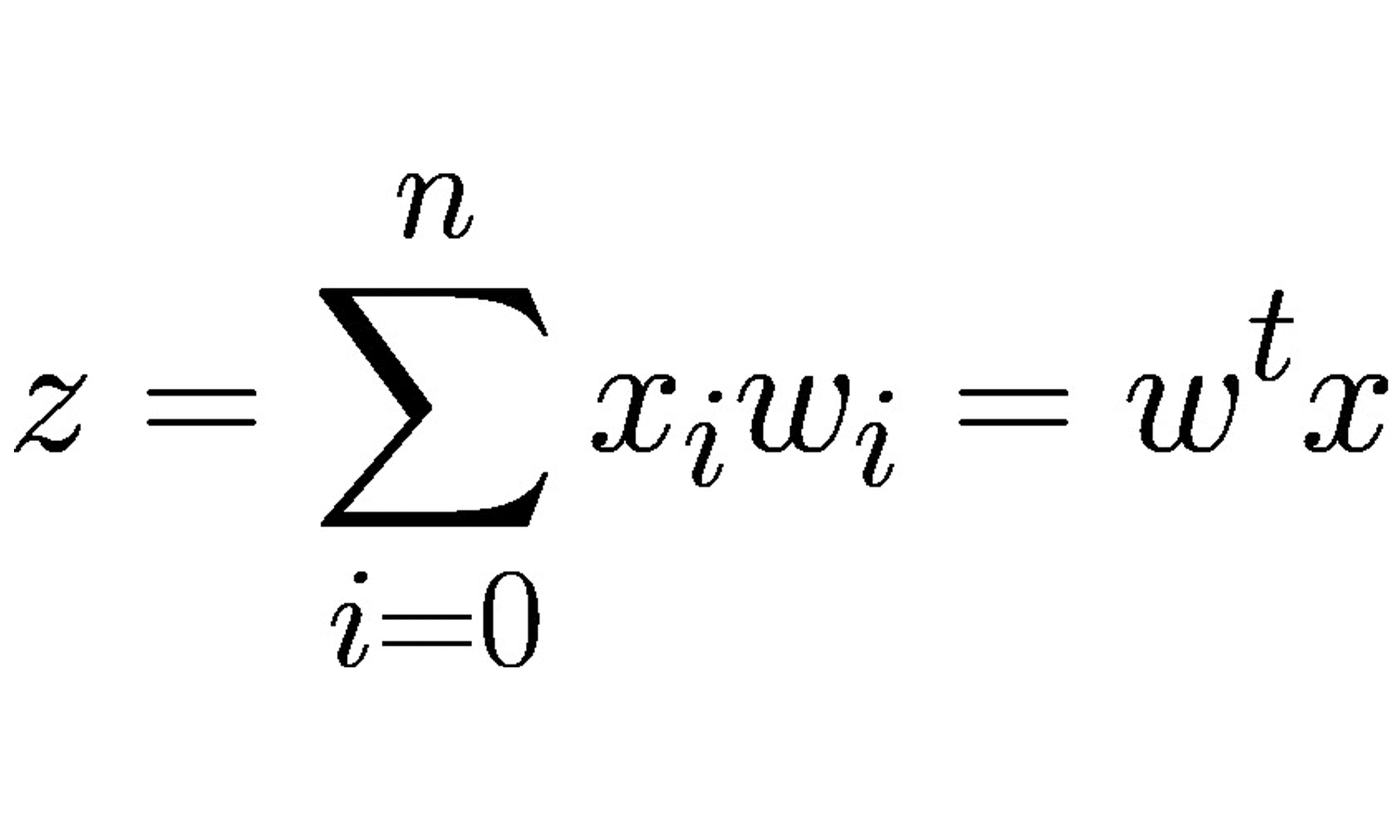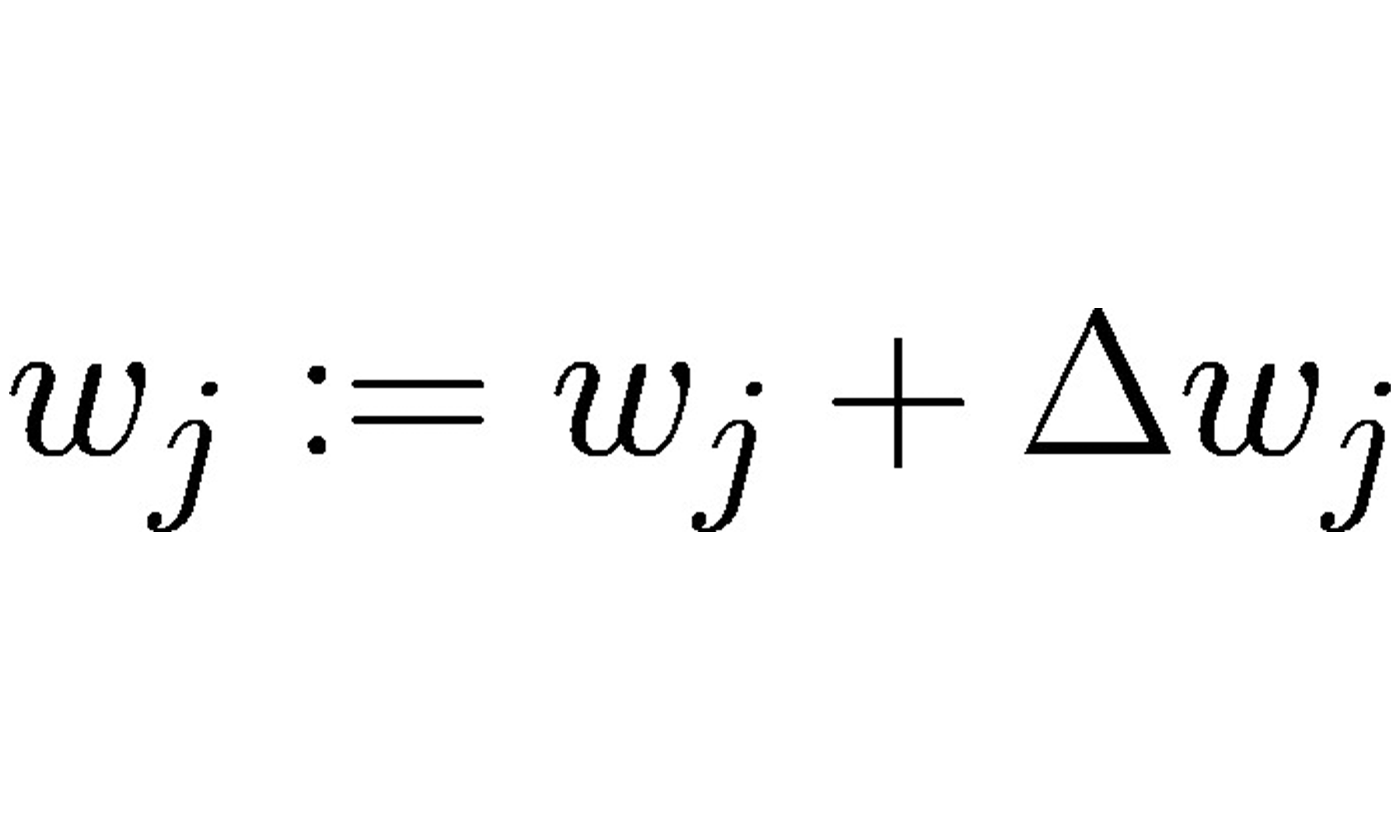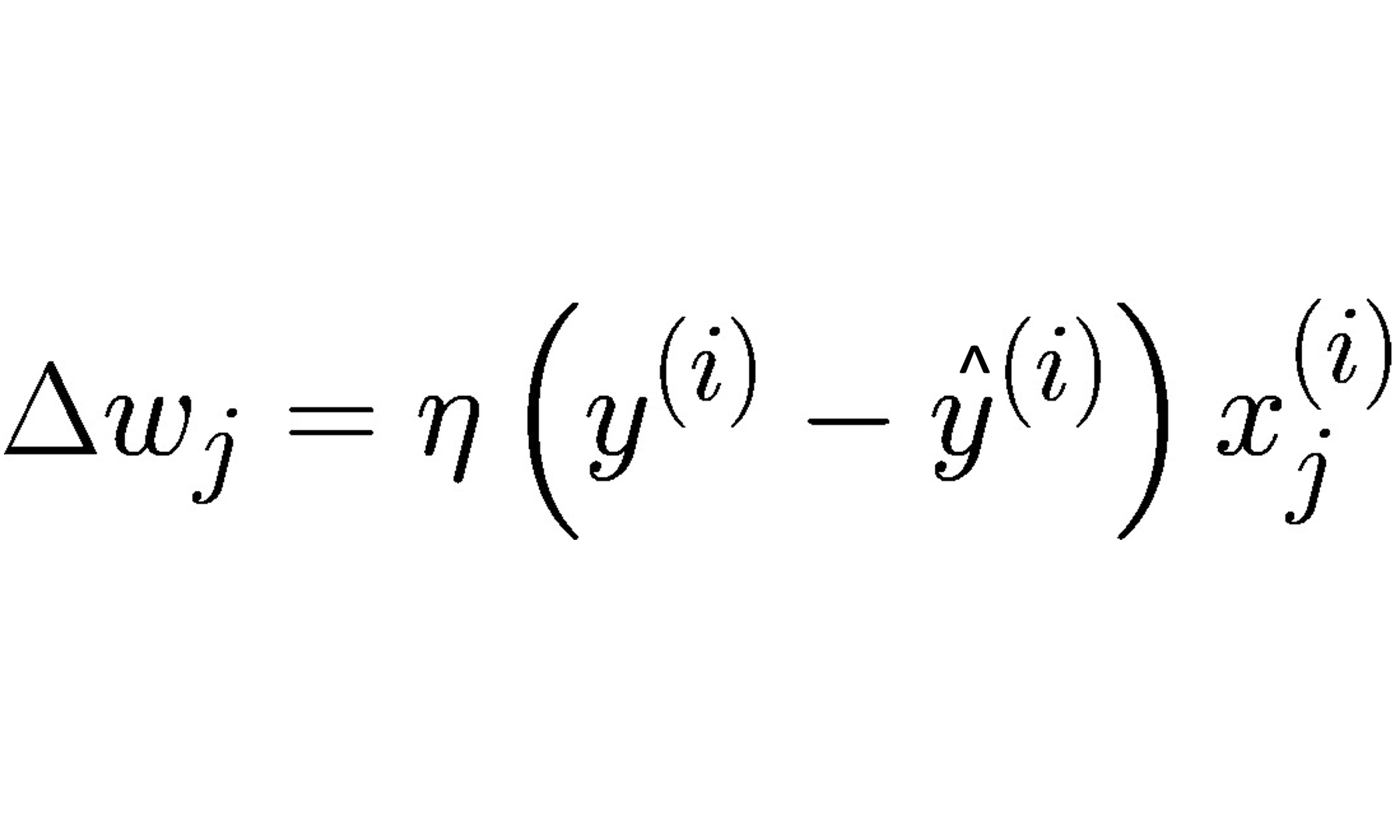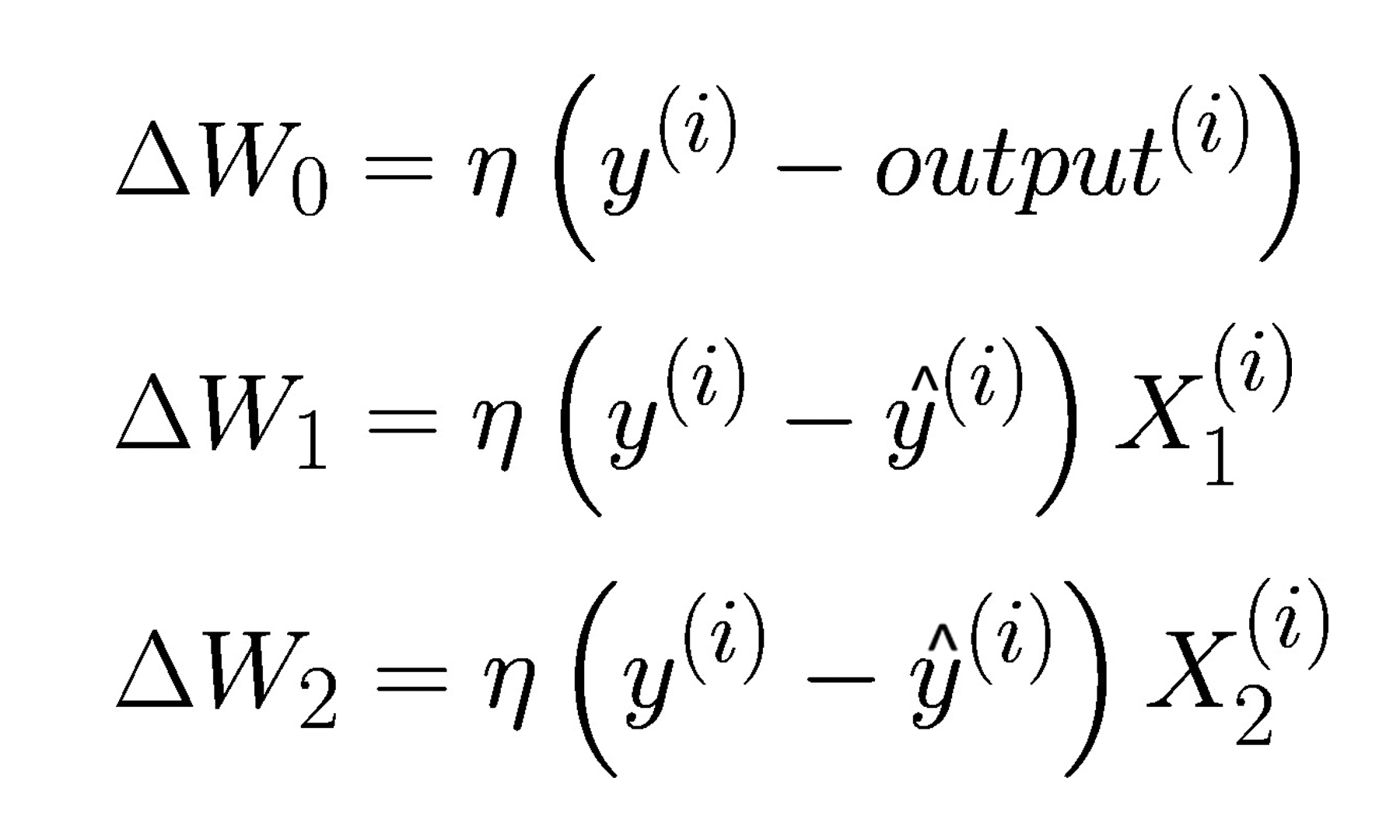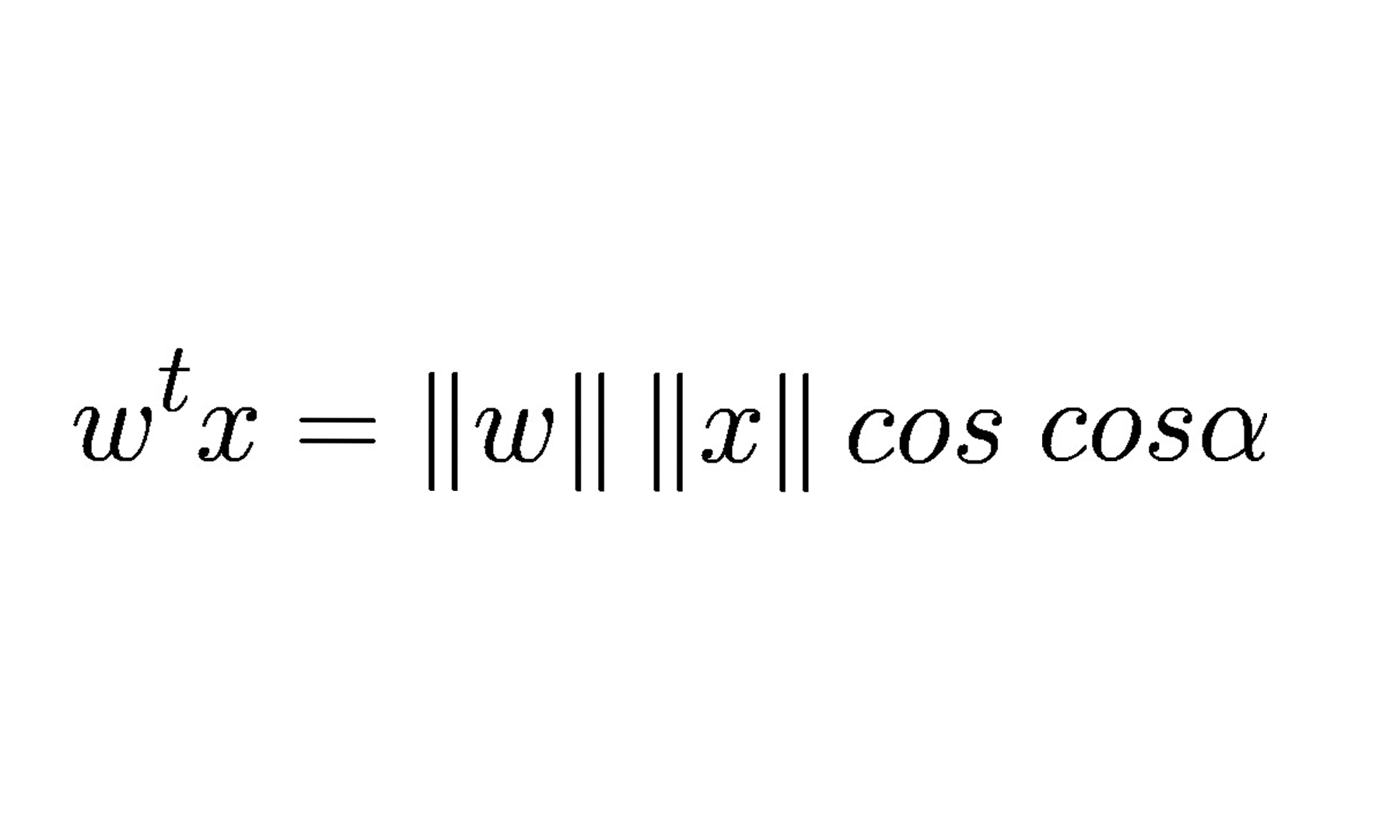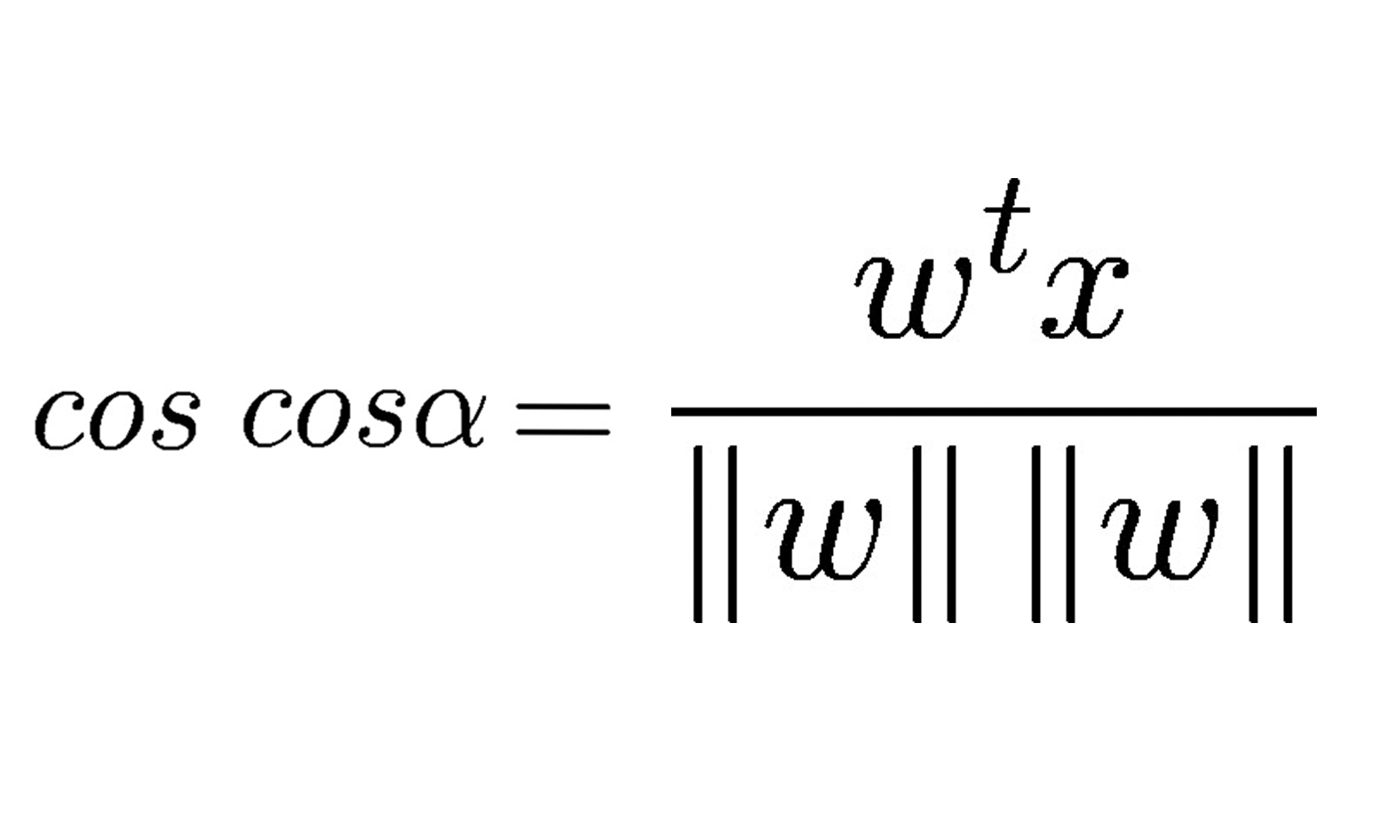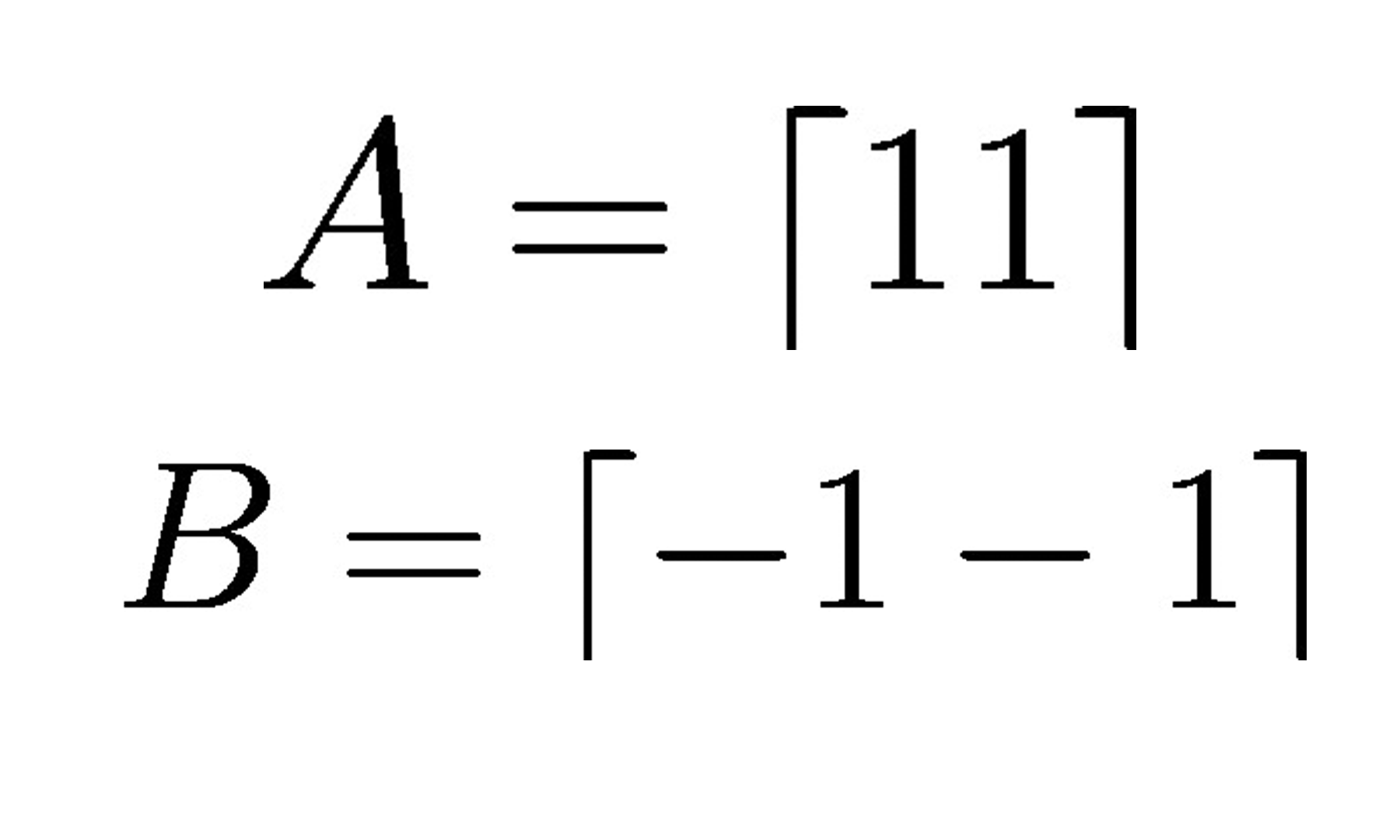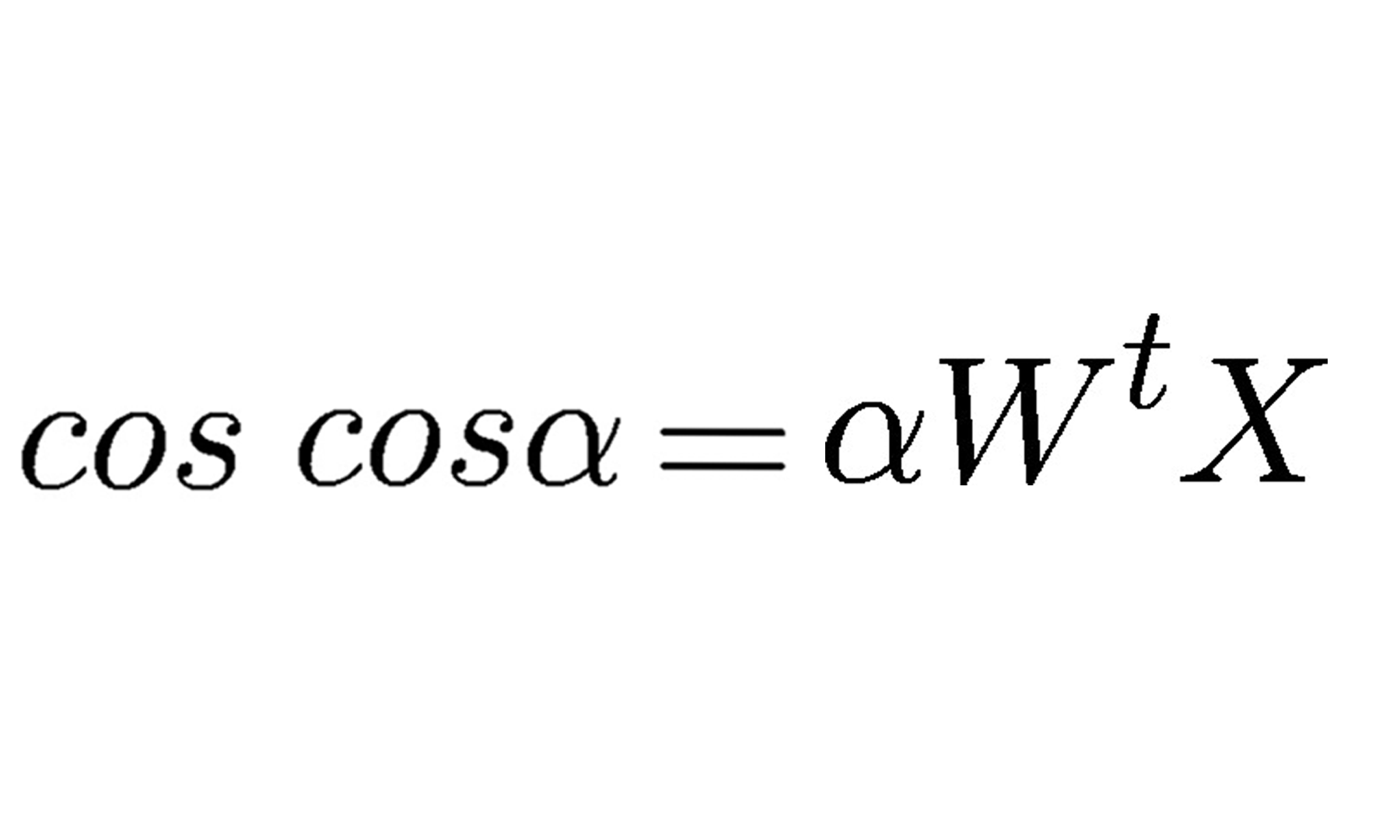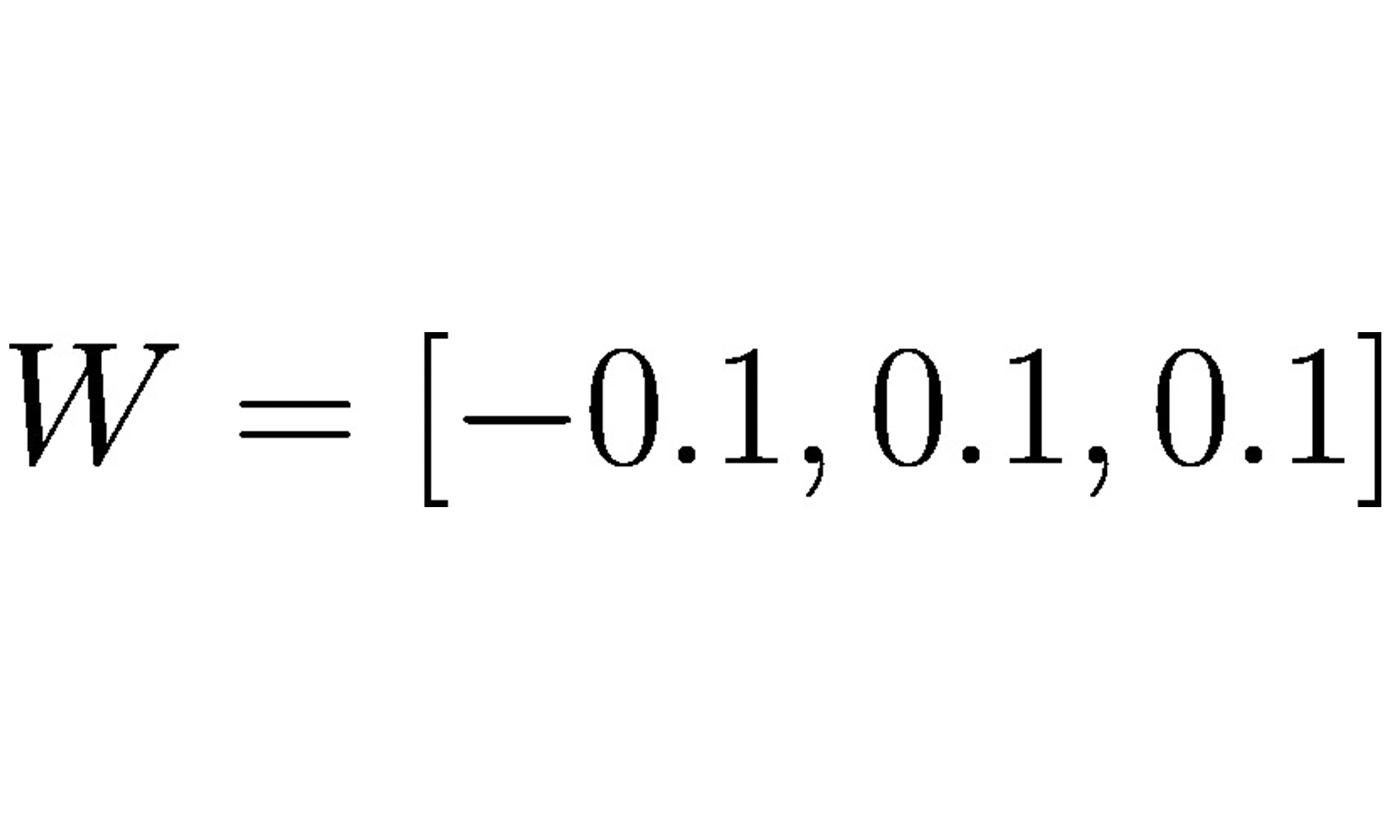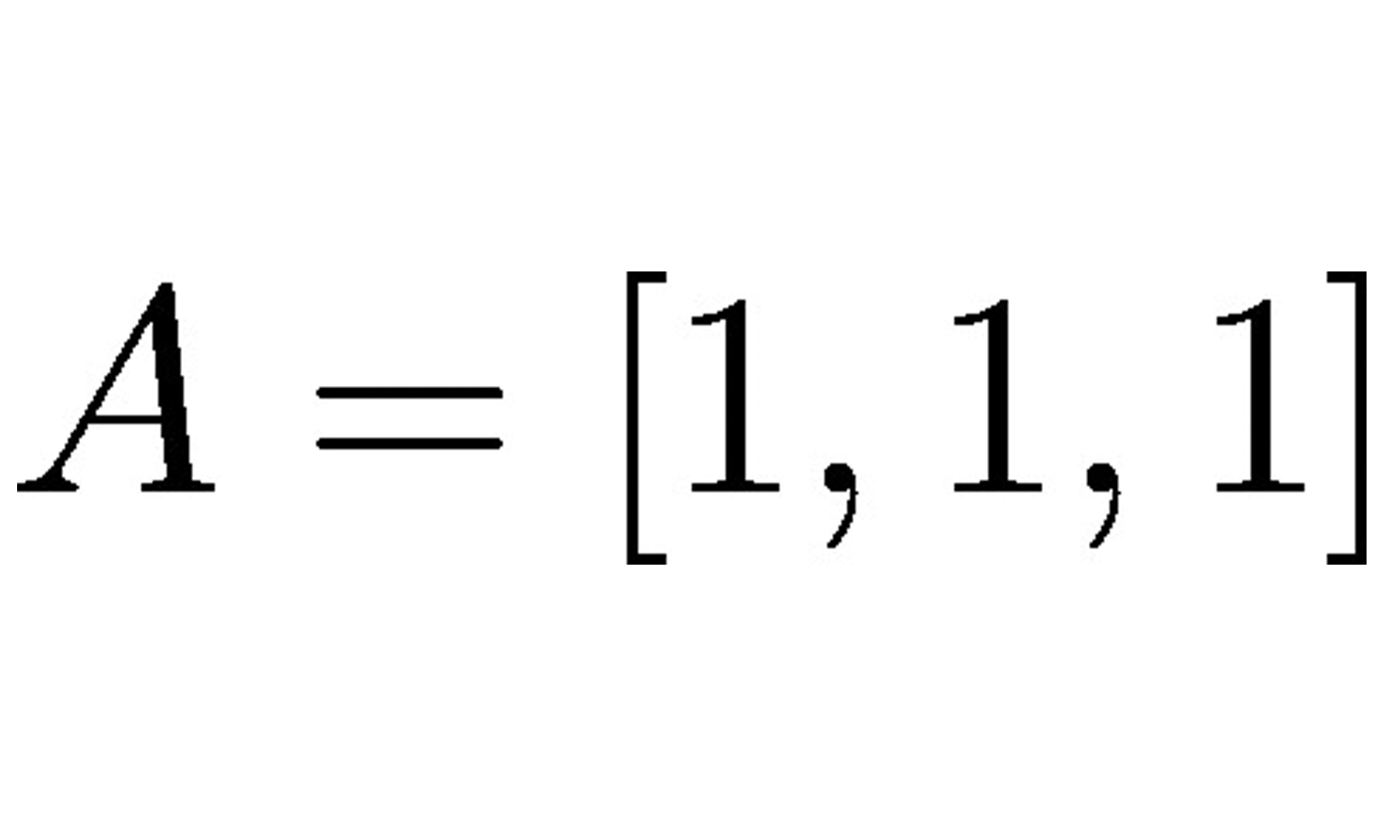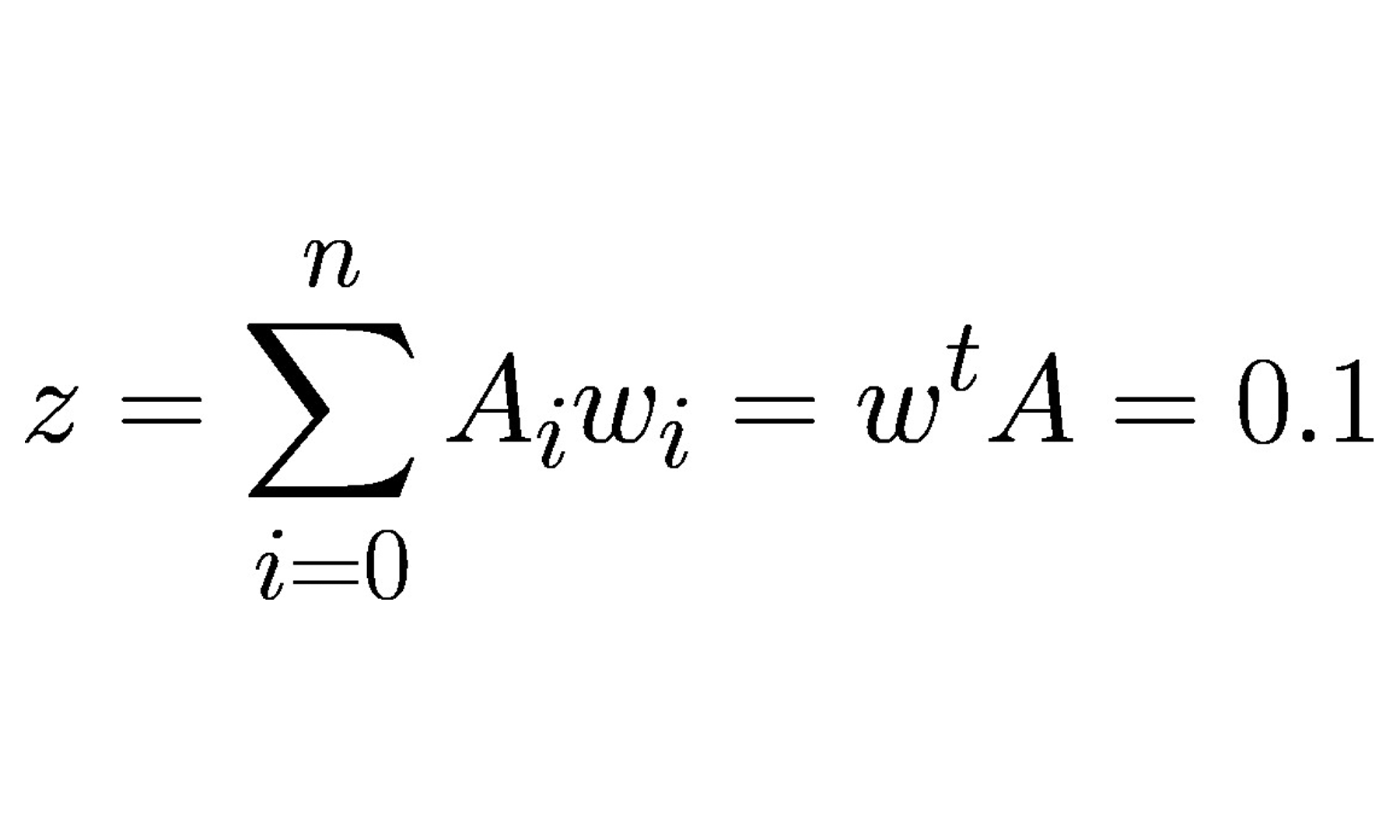14 fev. 2022
Neurônios Artificiais – Modelo Perceptron
Nas últimas semanas, publicamos o primeiro artigo da série de conteúdos sobre neurônio artificial. Hoje, vamos ver com um pouco mais de detalhes, ainda dentro do modelo perceptron, como um neurônio artificial deveria aprender a partir de um conjunto de dados.

Nysio Chrysostomo
Cientista de Dados I
blogAbstractMinutes
blogAbstractTimeReading

Intersetorial
DevOps
IA
contact
share
Na segunda parte da série sobre Neurônios Artificiais, explicamos o modelo perceptron e como ele funciona, com base em IA (Inteligência Artificial) e aprendizagem de máquina.
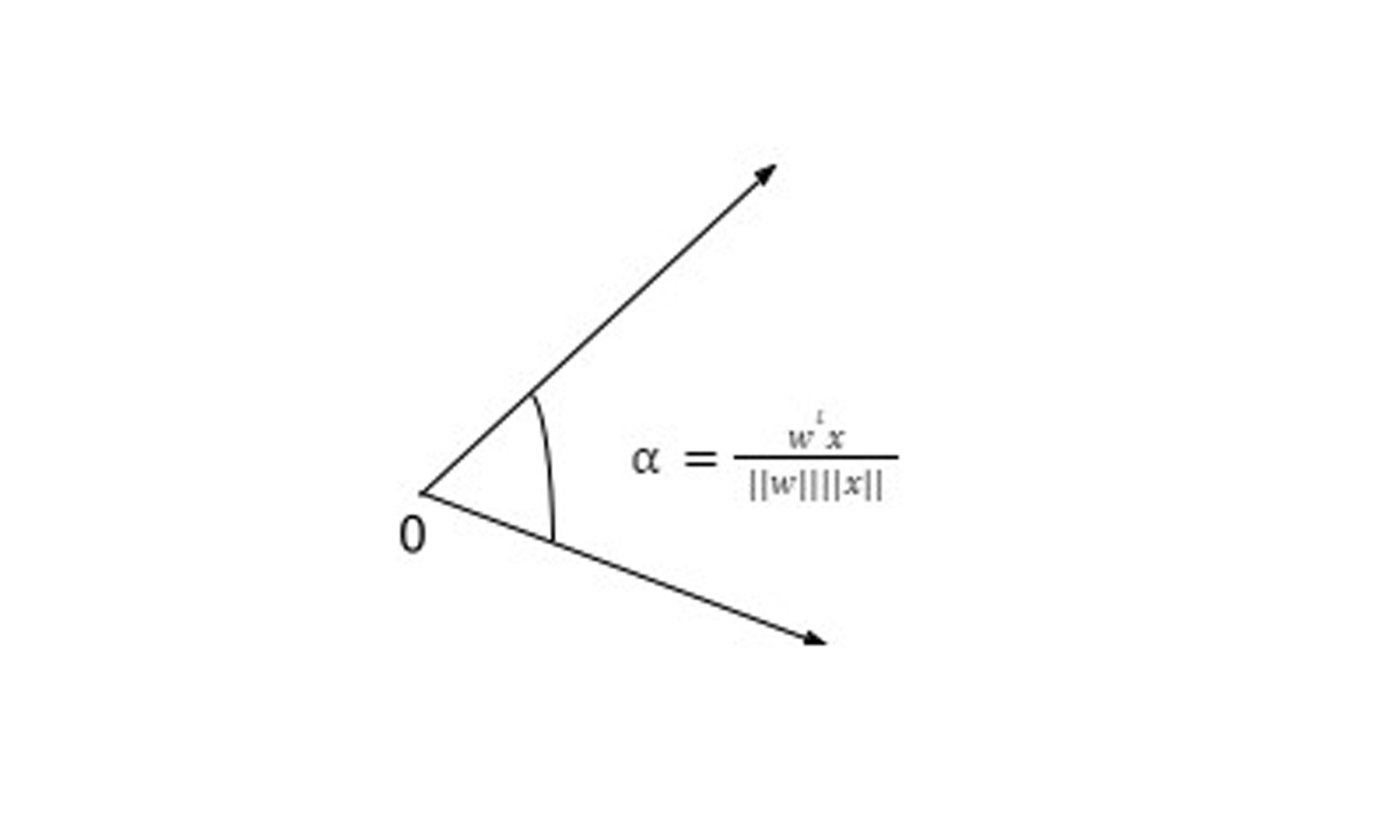
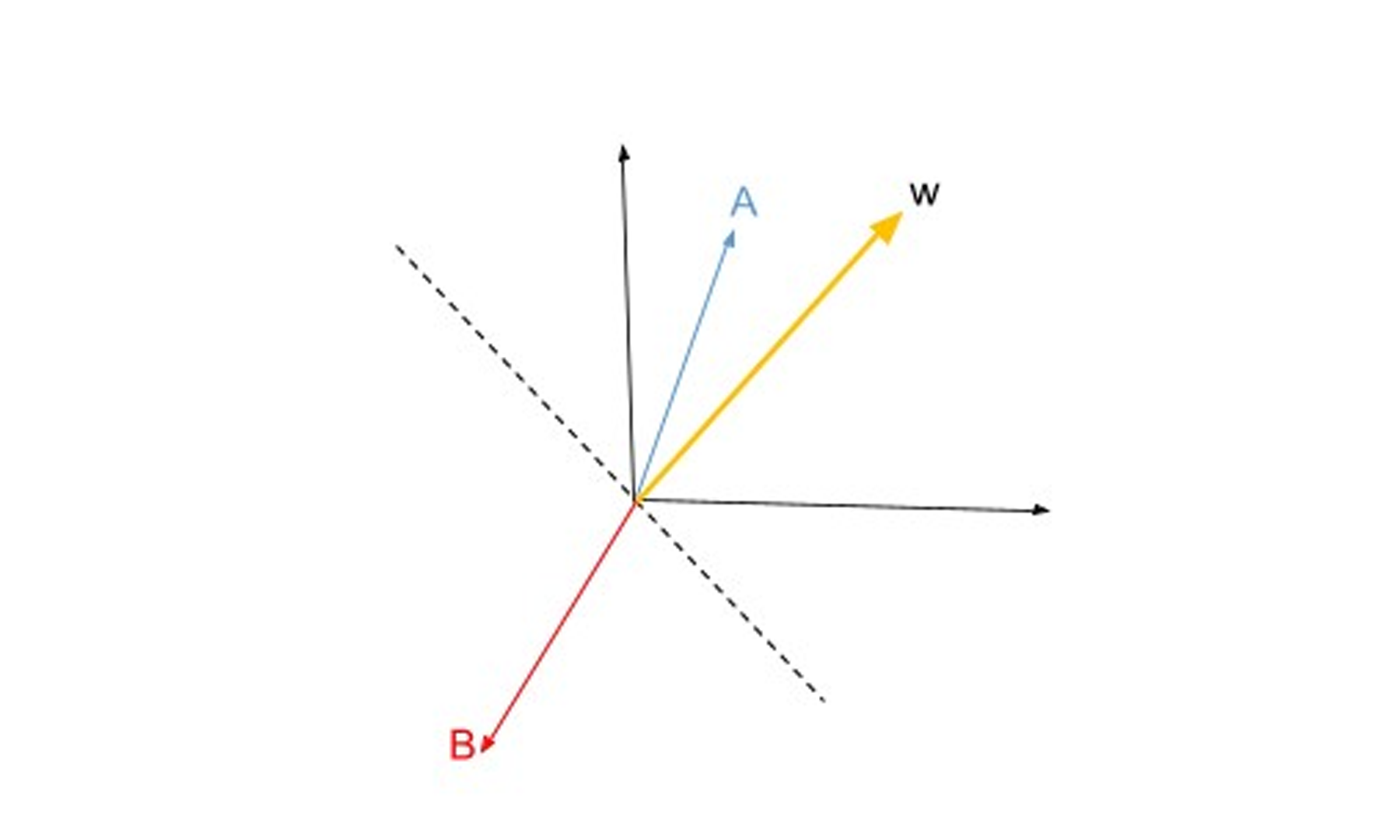
Continuando com o modelo de neurônio artificial, na visão de McCulloch-Pitts (MCP) e o limiar introduzido por Rosenblatt, vamos agora tratar da regra de aprendizagem dessa tecnologia. Podemos pensar que se trata de uma aproximação reduzida para simular como um neurônio biológico funciona dentro do cérebro, ou seja, se o neurônio vai ou não disparar um sinal de saída.